「Codeforces」CF 板刷记录

七点半的灯火，人潮将我吞没，连同我小小的歌。

CF1783E

难点在读题，一句话题意是对于两个元素大小在 $n$ 以内的序列 $a, b$ ，找到所有的 $k$ 能够满足 $\forall i \in [1, n], ⌊ \frac{a_{i}}{k} ⌋ \leq ⌊ \frac{b_{i}}{k} ⌋$ 。

假设我们已经对于每一对 $a_{i}, b_{i}$ 都求出了满足条件的 $k$ 的集合，对他们求交就可以得到整个序列的答案集合，那么只需要考虑怎么对 $a_{i}, b_{i}$ 求所有的 $k$ 即可。这个条件等价的可以转换成 $b_{i} \leq k x \leq a_{i} - 1$ ，于是可以差分预处理出来不能成为 $k$ 的倍数的数，于是可以直接枚举这样的 $k$ 的倍数，检查是否满足条件即可，复杂度 $Θ (n \log n)$ 。

CF1783F

考虑单个序列怎么做，这个东西是个置换，把所有的环扣出来即可，那么答案就是 $n - c n t$ ，其中 $c n t$ 是环的个数。

如果两个序列，同时操作需要保证两个环同时还原。再返回去看 $n - c n t$ 的来的过程，操作一次相当于把一个环的点数减一，而每个环都有一个不会动的点，于是可以通过这个不动点去同步两个序列，具体而言，对于 $i$ 在 $a$ 中的环记为 $c a_{i}$ ，同样地定义 $c b_{i}$ ，那么将 $c a_{i}$ 和 $c b_{i}$ 连边，跑最大匹配即可。

CF1749E

一道很有意思的建图题，使得这张图隔断的条件很简单，需要存在一条联通的栅栏，长度为 $m$ ，于是建边为： $(i, j)$ 向斜方向上的点连边，如果该点已经被放置，那么边权为 $0$ ，否则边权为 $1$ ，然后再弄起始节点，跑 $0 / 1$ 最短路就可以了，复杂度 $Θ (n m)$ 。

CF1749F

首先是一个很套路的分类，可以把子树内的贡献和子树外的贡献分开来考虑。

但是我并没有第一时间想到，因为受到了另外一道题的误导，这一道题大概算是弱化版，只用更新到某个点的距离不超过 $d$ 的节点的权值，这个时候就可以用 $b f s$ 序来维护，因为是一圈一圈的，还非常好写。

也可以发现这两道题本质不同的地方，在于数据范围，并且上一道限制了节点的度数小于 $2$ ，就不会被双重菊花图卡爆。

而这一道比较关键的地方在于 $k \leq 20$ ，可以盲猜这个会出现在复杂度里面。
显而易见的是把要把贡献叠到被计算的单点上，再结合第一个分类，往子树上贡献可以搞一个数据结构解决，往子树外贡献可以非常平凡的 $Θ (k)$ 暴力爬。

现在的问题是会算重，我想了半天就是不会，流汗。

接下来是形式化的题解。

定义 $s u m_{d, u}$ 为与 $u$ 结点距离为 $d$ 的在 $u$ 的子树内的节点的增值。

query： $\sum_{i = 0}^{d} s u m_{i, f a_{i, u}}$
update: 是一个迭代的过程，当前在节点 $u$ ，需要更新的距离为 $d$ ，那么重复以下操作 $s u m_{d, u} := s u m_{d, u} + Δ, s u m_{d - 1, u} := s u m_{d - 1, u} + Δ, d := d - 1, u = f a_{u}$ 。

然后把这个玩意搬到一条链上面，套上一个重链剖分，用树状数组维护就可以了。

CF1743F

感觉比 E 要难，但是评分低了。
拿到题感觉下不了手，观察到这个集合最大也只有 $3 e 5$ 个元素，那么可以套路地去给每一个元素计算贡献。

还是不会。。。

其实发现我们关心的是这个元素和当前操作集合是否有包含关系。分类讨论一下 $x$ 和 $S_{n}$ 的关系。

包含，那么在交和并操作之后依然包含。
不包含，那么在异或和并操作之后可以使得包含关系成立。

如果这个元素最后一次是被包含在了 $S_{k}$ 那么对于之前所有集合操作方式有 $2 \times 3^{k - 2}$ 使得这个元素被包含，对于之后的序列有 $2^{n - k + 1}$ 中操作序列，乘起来便是整个贡献。

现在我们需要求到这个 $k$ ，于是我们从前往后依次枚举每一条线段，每次查询 $[L, R]$ 中 $0$ 的个数，直接累加贡献，然后把区间赋 $1$ 。
注意要离散化或动态开点。

CF1821F

挺好一道题，可惜我是暴力二项式反演丑陋做法。

贪心的判定很显然，能往左边倒就往左边倒。先按计数 dp 方法写个式子， $d p_{i, j}$ 表示前 $i$ 棵树最后一棵倒下来放到了 $j$ 的方案数。

\begin{matrix} (1) & d p_{i, j} = \sum_{l = 0}^{j - k - 1} d p_{i - 1, l} + \sum_{l = j - 2 k}^{j - k - 1} d p_{i - 1, l} \end{matrix}

然后我对 GF 不怎么熟，就观察了一下这个式子，发现可以改写为

\begin{matrix} (2) & d p_{i, j} = 2 \sum_{l = j - 2 k}^{j - k - 1} d p_{i, l} + \sum_{l = 0}^{j - 2 k} d p_{i, l} \end{matrix}

继续观察，发现可以转化这个问题，对于一个长度为 $n$ 的序列分成 $m$ 段，使得每一段的长度都大于等于 $k$ ，当一段的长度大于 $2 k$ 时，该段的贡献为 $2$ 。

于是定义 $f_{i}$ 表示恰好有 $i$ 段的长度大于 $2 k$ 的方案数，则答案为 $\sum_{i = 0}^{m} 2^{m - i} f_{i}$ ，然后开始吟唱，定义 $g_{i}$ 表示至少 $i$ 段的长度大于 $2 k$ ，那么有下面的等式。

\begin{matrix} (3) & \begin{aligned} g_{i} & = \sum_{j = i}^{m} (\binom{m}{j}) f_{j} \\ = (\binom{m}{i}) (\binom{n - (i + m) k}{m}) \end{aligned} \end{matrix}

继续化简答案

\begin{matrix} (4) & \begin{aligned} r e s & = \sum_{i = 0}^{m} \sum_{j = i}^{m} (- 1)^{j} (\binom{j}{i}) g_{j} \\ = \sum_{j = 0}^{m} g_{j} \sum_{i = 0}^{j} 2^{m - j} (- 1)^{i - j} (\binom{j}{i}) \\ = \sum_{j = 0}^{m} (- 1)^{j} 2^{m - j} g_{j} \end{aligned} \end{matrix}

于是可以 $Θ (m)$ 直接计算了。

其实这个玩意没有这么复杂。可以有一个非常优美的 GF 做法，可惜我不会 /kk

CF1651F

高妙题，第一眼看上去是对塔分块，有一个比较暴力的 $Θ (n \sqrt{n})$ 的做法能冲过去。

正解就很神了，首先需要观察，一个怪兽能造成的贡献可以拆分成两种方式，第一种是一段区间直接推平，第二种是对于某一个塔削弱血量。考虑颜色段均摊，维护场上的若干个连续段 $[l, r]$ 。

如果遇到 $l = r$ ，直接暴力算。遇到 $l这代表被以前的询问推平的一段区间，问题成了给定初始生命 $h p$ ，时间差 $T$ ，左右端点 $[l, r]$ ，问是否能再次推平这个区间，或者是在这个区间停下。

比较关键的步骤是将塔的回血操作看成分段的一次函数，具体是

\begin{matrix} (5) & {\begin{cases} r_{i} t, & t \leq ⌈ \frac{c_{i}}{r_{i}} ⌉ \\ c_{i}, & t > ⌈ \frac{c_{i}}{r_{i}} ⌉ \end{cases} \end{matrix}

以位置为下标，可以上可持久化线段树，合并一次函数就行了。于是得到了一个主席树上二分的单 $l o g$ 做法。

CF1657F

明显是 2-sat 首先把路经抠下来，路经上第 $i$ 个点可以是 $s t r_{i}$ 或 $s t r_{l e n - i + 1}$ ，为表述方便，记为 $a, b$ ，将 $(a, b, x, y)$ 视为一个限制。

现在考虑如何合并两个限制，记另外一个限制为 $(c, d, x, y)$ ，讨论一下。

$a \neq c$ ：如果选 $a$ ，则强制另外一个限制路径用 $y \to x$ 满足限制，如果选了 $x \to y$ ，则只能选 $b$
$b \neq c$ ：如果选 $b$ ，则强制另外一个限制路径用 $x \to y$ 满足限制，如果选了 $y \to x$ ，则只能选 $c$
对于 $d$ ，同理，不写了

于是这是个点数为 $2 \times n m$ 的做法。

CF1661F

令 $d p_{l e n, x}$ 表示该区间长度为 $l e n$ ，增加 $x$ 个传送器后的代价。

观察一下，这个是个均值，所以每段最好分得尽量平均，有

\begin{matrix} (6) & \begin{array}{r} d p_{l e n, x} = (x - l e n \mod (x + 1) (⌊ \frac{l e n}{x + 1} ⌋)^{2}) + l e n \mod (x + 1) (⌈ \frac{l e n}{x + 1} ⌉)^{2} \end{array} \end{matrix}

再观察一下，发现 $d p_{l e n, x} - d p_{l e n, x}$ 有单调性，可以瞪眼大法知道是不增。然后可以直接二分这个减少的量记为 $Δ$ ，于是对每一段都求出来最大满足 $d p_{l e n, x} - d p_{l e n, x + 1}$ 的 $x$ ，于是增加 $Δ$ 个传送器的代价可以求得记为 $c o s t_{Δ}$ 。

似乎直接去求最大满足 $c o s t_{Δ} \leq m$ 的 $Δ$ 即可，但是这个 $Δ$ 不一定最优，我们可以在 $Δ + 1$ 的基础上继续增加，因为每增加 $1$ 个传送器，代价就会减少 $Δ$ ，所以算出来最少增加 $⌈ \frac{c o s t_{Δ + 1} - m}{d} ⌉$ 个。

CF1809F

首先看到 $b_{i} \in [1, 2]$ ，这明显是一个值得去发现性质的点。因为油箱容量不变（废话），所以遇到 $1$ 能加满就加满，只有在实在没油的情况下才会去加 $2$ 。发现这个合并并不是那么优美，因为每次剩下的油量都不一样，那么考虑每次都在油箱空了的时候去合并。

如果当前 $b_{i} = 1$
- 并且 $b_{i + 1} \neq 2$ ，直接交完当前需要的油钱，移动到下一个位置。
- 否则后面将会有 $l e n$ 个连续的 $2$ ，对于这一段区间记为 $[i + 1, i + l e n]$ ，记 $a_{i}$ 的前缀和数组为 $s u m$ ，需要二分出第一个 $p o s$ ，使得 $s u m [i + 1 \dots p o s] \leq k$ ，那么这一段区间的所有油都应该在 $i$ 处只花 $1$ 的代价加上，这是就会出现后面一段 $[p o s + 1, i + l e n]$ 的油不够，那么这一段只能花 $2$ 的代价买油。
如果当前 $b_{i} = 2$ ，直接交 $2 \times a_{i}$ ，往下移动。

于是得到了从每一个点出发走一步在最优情况下能够到达的位置记为 $n x t_{p o s, 0}$ ，显然这是一个倍增数组。

最后会发现一个小问题，在倍增完之后有可能到不了终点，并且这一段是连续的 $1$ ，那么直接计算两者之间的距离就能解决了。

CF1697F

又是 2-sat ，首先建出来 $a_{i} \to v$ 的边表示 $a_{i}$ 是否大于等于 $v$ ，有下面几个限制

$a_{i} \leq a_{i + 1}$ ， $\forall v$ ， $a_{i} \geq v \Rightarrow a_{i + 1} \geq v$
$a_{i} \neq x$ ， $a_{i} \geq x \Rightarrow a_{i} \geq x + 1$
$a_{i} + a_{j} \leq x$ ， $a_{i} \geq v \Rightarrow \neg (a_{j} \geq v - a_{i})$
$a_{i} + a_{j} \geq x$ ， $\neg (a_{i} \geq v) \Rightarrow a_{j} \geq v - a_{i}$

注意到不能忘记去建逆否命题的边，以及 $a_{i} \geq v \Rightarrow a_{i} \geq (v - 1)$ 。

CF1680F

首先二分图一定满足题目要求，否则该图中有奇环，删去的边一定要一键干掉所有的奇环，那么树上差分维护经过每个点的奇环就可以了。

CF1716 F

就是要求下面这个式子，开始吟唱

\begin{matrix} (7) & \begin{aligned} \sum_{i = 0}^{n} i^{k} (\binom{n}{i}) {(⌈ \frac{m}{2} ⌉)}^{i} {(⌊ \frac{m}{2} ⌋)}^{n - i} \\ = & \sum_{i = 0}^{n} \sum_{j = 0}^{k} j! {\begin{array}{c} k \\ j \end{array}} (\binom{i}{j}) {(⌈ \frac{m}{2} ⌉)}^{i} {(⌊ \frac{m}{2} ⌋)}^{n - i} \\ = & \sum_{j = 0}^{k} j! {\begin{array}{c} k \\ j \end{array}} \sum_{i = 0}^{n} (\binom{i}{j}) {(⌈ \frac{m}{2} ⌉)}^{i} {(⌊ \frac{m}{2} ⌋)}^{n - i} \\ = & \sum_{j = 0}^{k} j! {\begin{array}{c} k \\ j \end{array}} n^{\underset{―}{j}} {(⌈ \frac{m}{2} ⌉)}^{j} m^{n - j} \end{aligned} \end{matrix}

CF1709F

好吧，根本没读懂题，所以给一个看到的正常翻译。

一棵高度为 $n$ 的满二叉树（共 $2^{n + 1}$ 个点， $2^{n + 1} - 2$ 条边），边从父亲指向儿子。

每条边的最大流量为 $[0, k]$ 内的整数，求有几种赋最大流量方案，使得以根为源点，所有叶子为汇点，最大流恰好为 $f$ 。

令 $d p_{x, f}$ 表示现在从下往上流回第 $x$ 层，最大流量是 $f$ 的总方案数，因为每一层的 $d p$ 值是一样的，所以说只需要对 $n$ 个点进行计算就可以了。那么往上计算，对于两个子结点 $u, v$ 往 $f a$ 转移的时候，限制的因素要么是 $f a$ 处的流量，要么是 $u$ 和 $v$ 的流量和。

写出转移方程

\begin{matrix} (8) & \begin{array}{r} d p_{f a, c} = \sum_{i + j > c} (d p_{u, i} \cdot d p_{v, j}) + \sum_{i + j = c} (k - c + 1) (d p_{u, i} \cdot d p_{v, j}) \end{array} \end{matrix}

注意到 $d p_{u, \dots}$ 和 $d p_{v, \dots}$ 是一个东西，于是 $d p_{u, i} \cdot d p_{v, j} = d p_{u, i + j}$ 。于是调整一下这个式子变成

\begin{matrix} (9) & \begin{aligned} d p_{f a, c} = \sum_{i = c + 1}^{2 k} d p_{u, i} + (k - c + 1) d p_{u, c} \end{aligned} \end{matrix}

因为 $d p_{u, i} \cdot d p_{v, j} = d p_{u, i + j}$ 是个卷积形式。

那么令 $G$ 是上一层的生成函数， $F$ 是这一层的生成函数，那么 $G = F^{2}$ ，直接 NTT 解决即可。

CF1795F

考虑对于一个固定的步数，构造出来一个唯一的方案。

操作是有顺序的，必须按照 $1, 2, 3, \dots, k$ 的顺序走，那么在总步数为 $s$ 的约束下，每一个棋子的步数可以确定，记为 $c n t_{i}$ ，于是递归去处理这个问题，记每一个位置目前能够往下（深度更大）走的最大距离为 $t o t_{u}$ 对于当前位置的 $u$ ，如果 $t o t_{u} \geq c n t_{i}$ ，直接把它放下去，否则往上挪，如果父结点也有棋子或者它本身是根，那么无法完成要求。于是二分即可。

CF1809G

每次在末尾添加一个元素的时候，关心的只有前面所有元素的最大值，因为 $n \in [1, 1 e 6]$ ，并且不可能去记录现在剩下来的最大值，所以猜测这个计数往后添加时一定是有一个明确的顺序的。

考虑到这个状态只能一维地去定义，那么就必须保证每一步填完之后这个数列都合法，就是说 要让当前数列开头的数和剩下的数无论怎么填都合法 ，定义 $d p_{i}$ 表示已经填了前面第 $i$ 大的元素，那么第 $i + 1$ 大的元素有两种填法。

不成为第一个数， $d p_{i + 1} := d p_{i + 1} + d p_{i} \times i$
成为第一个数，这样会有冲突，是 $[i + 2 \dots t o [i] - 1]$ 连续的一段应该也一起放，这样保证状态还是合法的。 $d p_{t o [i + 1] - 1} := d p_{i} \times (i \times \dots \times t o [i + 1] - 3)$

CF1814F

线段树分治。判断是否和 $1$ 联通，直接在并查集上打标记就可以了，注意下传的时候撤销。

CF997C

考虑容斥，定义 $f (x, y)$ 表示至少有 $x$ 行， $y$ 列被染成了同样的颜色的方案数。
分类讨论一下，得到

\begin{matrix} (10) & \begin{array}{r} f (x, y) = {\begin{cases} (\binom{n}{x + y}) 3^{(n - x - y) n + x + y}, & x y = 0, x + y \neq 0 \\ (\binom{n}{x}) (\binom{n}{y}) 3^{(n - x) (n - y) + 1} & x y \neq 0, x + y \neq 0 \\ 3^{n^{2}} & x y = 0, x + y = 0 \end{cases} \end{array} \end{matrix}

进行一个二维的反演，定义 $g (x, y)$ 表示恰好有 $x$ 行， $y$ 列被染成了同样的颜色的方案数。

\begin{matrix} (11) & \begin{aligned} f (x, y) = \sum_{i = 0}^{n} \sum_{j = 0}^{n} (\binom{n}{i}) (\binom{n}{j}) g (i, j) \\ \Leftrightarrow & g (x, y) = \sum_{i = x}^{n} \sum_{j = y}^{n} (\binom{x}{i}) (\binom{y}{j}) (- 1)^{(i + j) - (x + y)} f (i, j) \end{aligned} \end{matrix}

用总方案数减去 $g (0, 0)$ 就是答案，现在来求 $g (0, 0)$ 。

\begin{matrix} (12) & \begin{aligned} g (0, 0) & = \sum_{i = 0}^{n} \sum_{j = 0}^{n} (- 1)^{i + j} f (i, j) \\ = f (0, 0) + (\sum_{i = 1}^{n} f (0, i) + f (i, 0)) + \sum_{i = 1}^{n} \sum_{j = 1}^{n} (- 1)^{i + j} f (i, j) \\ \sum_{i = 1}^{n} \sum_{j = 1}^{n} (- 1)^{i + j} f (i, j) \\ = & \sum_{i = 1}^{n} \sum_{j = 1}^{n} (- 1)^{i + j} (\binom{n}{i}) (\binom{n}{j}) 3^{(n - i) (n - j) + 1} \\ = & 3 \sum_{i = 1}^{n} (- 1)^{i} (\binom{n}{i}) \sum_{j = 1}^{n} (- 1)^{j} (\binom{n}{n - j}) {(3^{n - i})}^{(n - j)} \\ = & 3 \sum_{i = 1}^{n} (- 1)^{i} (\binom{n}{i}) (3^{n - i} - 1)^{n} \end{aligned} \end{matrix}

于是可以 $Θ (n)$ 计算了。

CF679E

从最难处理的操作入手，如何判断一个区间中存在 $42$ 的次幂？如果单纯地去维护每个数的真实值，则会出现问题：没有一个统一的标准检验是否是 $42^{x}$ ，因为每个数处于不同的由 $42$ 的次幂分割出来的区间之中。
转换一下，维护每个数与它最近的 $42$ 次幂的差值，这样我们只需要检验数列中是否存在 $0$ 就行了。
出现另外一个问题，在重复做 3 操作的过程中有可能出现负数，这意味着这个数跨越了一个 $42$ 的次幂，我们必须单独去更新它。
考虑这个做法的复杂度， $42$ 的次幂在可能的值域中 $V = max {a_{i}} \times q = 1 e 14$ 最大只能在 $9$ 次方左右，也就是说，每个数最多只会跨过 $9 = \log_{42} V$ 次，但是做 2 操作会出现 $Θ (1)$ 个连续段，增加 $\log_{42} V$ 的势能，结合到每次操作是 $Θ (\log n)$ 的，所以总的时间复杂度是 $Θ ((q + n) \log_{42} V \log n)$ 。

CF1588F

好神的题，但也并非没有突破口。
发现这里既有图上的又有序列上的操作，非常抽象🤔，思考能不能分块，对谁分块。
因为操作过于复杂，那就对操作分块，于是我们现在得到了 $\sqrt{q}$ 个块，每个块里面有 $\sqrt{q}$ 个操作，我们需要在 $Θ (n)$ 左右的复杂度内解决每个块里的询问。
最恶心的操作是操作 3，出现了改边。结合到分块的原理，块内的元素相当于是等价的，他们的行为是平行的，而在操作 3 里面出现的点都经历了改边的步骤，所以他们的行为一定互相不平行，钦定他们为关键点，记换上的一部分为 $v_{1}, v_{2}, \dots, v_{k}, x, v_{k + 2}, v_{k + 3}, \dots, y, \dots$ ，其中 $x$ 和 $y$ 是被标记的关键点，那么可以知道 $v [1 \dots x]$ 可以放在一个块里面， $v [k + 2, y]$ 可以放在一个块里。
就像是这样

怎么想到的，为啥是对的？
其实很明显，因为 $x, y$ 有改边的操作，那么对于环上连在 $x$ 后面的点来说， $x$ 可以作为一个 leader， $x$ 后面的点的行为都是由 $x$ 指挥进行的。简单看一下，对于每一次拎出来的 $\sqrt{q}$ 操作，最多会有 $2 \sqrt{q}$ 个 leader 出现，意味着块的个数是 $\sqrt{q}$ 级别的。
这样看起来复杂度就对了，于是思考操作一怎么做，可以拆开一个询问，把区间和变成前缀和做差，那么只需要统计每个块中有多少个点出现在了询问中即可，这一步是 $Θ (n)$ 的。
操作二直接跳环上关键点，这一步是 $Θ (\sqrt{n})$ 的，操作三直接改即可。
因为 $n, q$ 同阶，所以总的复杂度是 $Θ (n \sqrt{n})$ 的。

代码确实不好写，还要多看几遍。

/*
If the radiance of a thousand suns were to burst into the sky?
...that would be like the splendor of the mighty one.
*/
#pragma GCC optimize("Ofast,no-stack-protector")
#pragma GCC target("avx2,fma")
#include <cmath>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#define LL long long
#define ULL unsigned long long
using namespace std;
const int MAXN = 2e5 + 5;
const int MAXM = 600;

template <typename T>
inline void read(T& x) {
  x = 0; int f = 1; char c = getchar(); while (c < '0' || c > '9') { if (c == '-') f = -f; c = getchar(); }
  while (c >= '0' && c <= '9') { x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); } x *= f;
}
template <typename T, typename... Args>
inline void read (T &x, Args&... Arg) { read (x), read (Arg...); }
template <typename T>
inline T Abs(T x) { return x < 0 ? -x : x; }
template <typename T>
inline T Max(T x, T y) { return x > y ? x : y; }
template <typename T>
inline T Min(T x, T y) { return x < y ? x : y; }

int n, q, m, cnt, siz, ind, tp,nxt[MAXN], col[MAXN], ed[MAXN], stk[MAXN];
struct Node { int opt, x, y, ind; } que[MAXN], ask[MAXN];
vector<int> pos;
bool vis[MAXN];
LL sum[MAXN], add[MAXN], num[MAXM][MAXM], a[MAXN];

inline void solve(int m) {

  ind = 0, cnt = 0, pos.clear();
  memset(vis, 0, sizeof(vis)), memset(col, 0, sizeof(col));
  memset(num, 0, sizeof(num)), memset(add, 0, sizeof(add));
  for (int i = 1; i <= m; i++) {
    if (que[i].opt == 1) {
      if (que[i].x > 1) ask[++cnt] = Node{-1, que[i].x - 1, 1, i};
      ask[++cnt] = Node{+1, que[i].y, 1, i};
    } else if (que[i].opt == 2) vis[que[i].x] = true;
    else vis[que[i].x] = vis[que[i].y] = true;
  }

  for (int i = 1, now; i <= n; i++) if (vis[i]) {
    pos.push_back(i), now = i;
    do { stk[++tp] =  nxt[now], now = nxt[now]; } while (vis[now] != true);
    ed[pos.size()] = stk[tp]; while (tp) col[stk[tp--]] = ed[pos.size()];
  }
  sort(ask + 1, ask + 1 + cnt, [](const Node& x, const Node& y) { return x.x < y.x; });

  for (int i = 1; i <= cnt; i++) {
    while (ind < ask[i].x) add[col[++ind]]++;
    for (int j = 1; j <= (int)pos.size(); j++) num[ask[i].ind][j] += ask[i].opt * add[ed[j]];
  }

  memset(add, 0, sizeof(add));
  for (int i = 1, now; i <= m; i++) {
    if (que[i].opt == 1) {
      LL res = sum[que[i].y] - sum[que[i].x - 1];
      for (int j = 1; j <= (int)pos.size(); j++) res += num[i][j] * add[col[ed[j]]];
      printf("%lld\n", res);
    } else if (que[i].opt == 2) {
      now = col[que[i].x];
      do { add[now] += que[i].y, now = col[nxt[now]]; } while (now != col[que[i].x]);
    } else swap(nxt[que[i].x], nxt[que[i].y]);
  }
  for (int i = 1; i <= n; i++) a[i] += add[col[i]], sum[i] = sum[i - 1] + a[i];

}

int main() {

  read(n);
  for (int i = 1; i <= n; i++) read(a[i]), sum[i] = sum[i - 1] + a[i];
  for (int i = 1; i <= n; i++) read(nxt[i]);

  read(q), siz = sqrt(q);
  for (int i = 1; i <= q; i++) {
    m++, read(que[m].opt, que[m].x, que[m].y);
    if (m == siz) solve(m), m = 0;
  }
  if (m > 0) solve(m);

  return 0;
}

CF1458D

从操作的限制入手，要求是“连续子串必须包含同样数量的字符 0 与 1”。
将 $0$ 换成 $- 1$ ，然后记录前缀和，并建图，对于每一个 $i$ ，都建一条 $s_{i} \to s_{i + 1}$ 的边，如果 $[l, r]$ 这一段能够操作，那么 $s u m_{l - 1} = s u m_{r}$ 。
之后的方法就很妙了，如果我们对 $[l, r]$ 操作，那么 $s u m_{l \dots r}$ 会发生改变，似乎没办法维护，但是观察性质可以《发现》：如果说操作前前缀和变化的顺序是从前往后，那么操作之后前缀和的变化是从后往前。
把这个放到图上去，相当于把 $[l, r]$ 这一段里面的所有边都反向。于是现在得到的问题就变成了求一条字典序最短的欧拉通路，贪心很显然。

CF827F

拿到题的第一时间注意到了不能原地停留，而每条边有出现的时间区间，马上想到可以反复横跳。
于是要分奇偶讨论，对于每个点记录 $f_{u, 0 / 1}$ 表示最晚能够在 $u$ 的时间，因为每条边有特定的通过时间，考虑以 $l_{i}$ 升序排序，去掉时间这一维度。那么 $f_{u, 0 / 1}$ 一定是由时间更小的边走过来的，在当前边出现的时候是一定能走的。
对于有一些目前还不能走的边 $f_{u, 0 / 1} < l$ ，可以把它挂在 $u$ 这个点上面，直到 $f_{u, 0 / 1} \geq l$ 之后再将它放到边集里面去。因为每条边最多会被塞到边集里面两次，所以复杂度是 $Θ (m \log m)$ 的。

CF1307F

不难想到要把点的询问挂到对于它最优的休息点上去，于是预处理每个休息点能够辐射到的范围，发现有一些休息点能够互相覆盖，希望将他们塞到一个并查集里面去。
那么有了第一步，从每个休息点出发走 $\frac{k}{2}$ 步，记录每个点最近的休息点，并将能够互相走到的点塞入一个并查集中。
说得有点抽象，代码如下

inline void spread() {
  for (int u : sp) que.push(mp(u, 0)), pre[u] = u;
  while (!que.empty()) {
    pii now = que.front(); que.pop(); int u = now.first;
    if (now.second >= k >> 1) continue;
    for (int v : G[u]) {
      if (!pre[v]) pre[v] = pre[u], que.push(mp(v, now.second + 1)), dsu.unionset(v, pre[u]);
      else dsu.unionset(pre[v], pre[u]);
    }
  }
}

然后考虑回答每一个询问，对于二元组 $(u, v)$ ，若 $dist (u, v) \leq k$ 那么可以直接走到，否则需要经过休息站。于是从 $u$ 往 $lca (u, v)$ 跳 $\frac{k}{2}$ 步到 $x$ ，从 $v$ 往 $lca (u, v)$ 跳 $\frac{k}{2}$ 步到 $y$ 。如果 $x, y$ 能够互通，那么 $u, v$ 能够互通。
接下来论证这个方法的正确性，即是论证 $x$ 能走到的有用的休息站集合和 $u$ 能走到的有用的休息站集合等价，只需要想，如果有一个休息站 $p$ ， $u$ 能走到， $x$ 不能走到，这就意味着 $dist (p, x) > k, dist (p, u) \leq k$ ，因为 $dist (u, x) = dist (p, x) = dist (p, u) = \frac{k}{2} \Rightarrow dist (p, u) > \frac{k}{2}$ ，所以先走到 $p$ 再走到 $x$ 只会更劣，同理 $v, y$ 也能得出一样的结论。

这里有一些小细节需要注意，为了避免小数距离，可以将 $k$ 乘一倍，在边之间塞虚点；如果往上跳的时候 $dist (u, lca (u, v)) < \frac{k}{2}$ ，相当于让 $v$ 往上面跳 $dist (u, v) - \frac{k}{2}$ 步。

CF1556G

删除不是很好实现，首先时光倒流，转换成添加操作。

第一步很难，需要把数放到线段树结构上去做。
可以发现一棵子树内都是联通的，于是可以用这棵子树的根节点代表整棵子树进行操作。

在线段树上记录每个点被删除的时间，可以直接打标记实现，然后遍历每一个不是“叶节点”的点，将其内部暴力连边，若该边连接了 $u, v$ 两个点，那么该边出现的时间是 $min (rm (u), rm (v))$ ，并将它加入此时间的边集里。
处理询问时，倒序往前把删掉的边塞入并查集，每次查询只需要问能代表 $a_{i}, b_{i}$ 的节点是否联通即可。

CF1383E

CF678F

如果没有删除，直接李超树上就可以了。考虑离线，线段树分治来做，维护每对 $(x, y)$ 出现的范围，直接给每个叶子节点建一颗动态开点李超树。
因为时间比较久远~~通过代码头部注释内容判断~~，放个代码自己复习一下。

int n, cnt, re[MAXN], pos[MAXN];
struct Range { int l, r; } ra[MAXN];
struct Opt { int k, ind, x, y; } opt[MAXN];
struct Line { int x, y; } li[MAXN];

inline int getval(int ind, int k) { return k * li[ind].x + li[ind].y; }
struct LichaoTree {
  int tot, root[MAXN * MAXM];
  struct Node { int l, r, dat; } s[MAXN * MAXM];
  inline void insert(int& p, int l, int r, int ind) {
    if (!p) p = ++tot;
    if (!s[p].dat) return s[p].dat = ind, void();
    int mid = (l + r) >> 1;
    if (getval(ind, mid) > getval(s[p].dat, mid)) swap(s[p].dat, ind);
    if (getval(ind, l) > getval(s[p].dat, l)) insert(s[p].l, l, mid, ind);
    else if (getval(ind, r) > getval(s[p].dat, r)) insert(s[p].r, mid + 1, r, ind);
  }
  inline int query(int p, int l, int r, int k) {
     if (!p) return -INF;
     if (l == r) return getval(s[p].dat, k);
     int mid = (l + r) >> 1, res = getval(s[p].dat, k);
     if (k <= mid) res = Max(res, query(s[p].l, l, mid, k));
     else res = Max(res, query(s[p].r, mid + 1, r, k));
     return res;
  }
} lt;
struct SegmentTree {
  struct Node { int l, r; } s[MAXN << 2];
  inline void build(int p, int l, int r) {
    s[p] = Node{l, r};
    if (l == r) return pos[l] = p, void();
    int mid = (l + r) >> 1;
    build(p << 1, l, mid), build(p << 1 | 1, mid + 1, r);
  }
  inline void update(int p, int l, int r, int ind) {
    if (s[p].l >= l && s[p].r <= r) {
      lt.insert(lt.root[p], -LIM, LIM, ind);
      return;
    }
    int mid = (s[p].l + s[p].r) >> 1;
    if (l <= mid) update(p << 1, l, r, ind);
    if (r > mid) update(p << 1 | 1, l, r, ind);
  }
} seg;

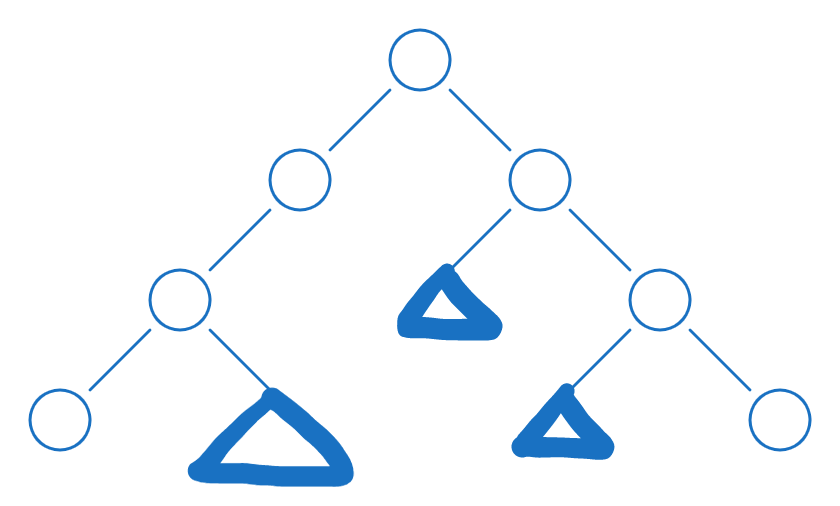
CF1149C

首先考察一下括号序列和树的直径的关系，给左括号赋值为 $1$ ，给右括号赋值为 $- 1$ ，设 $x, y$ 分别为树的直径的两个端点，结合图看一下发现

以三角形符号代替的子树都会自行内部括号匹配消化，于是直径就相当于把括号序列中匹配的中间匹配的括号扣掉之后不能被匹配的括号数。

相当于找一条分界线，求右边的最大字段和，求左边的最小字段和，然后做差。
因为我会 GSS 3 - Can you answer these queries III，所以这道题我一眼秒了，然后 WA * 3。因为有点细节，放一下部分代码。

struct Element {
  int dat, lmax, rmax, lmin, rmin, sum, maxl1, maxl2;
  inline Element operator + (const Element oth) {
    Element res;
    res.sum = sum + oth.sum;
    res.lmax = Max(lmax, sum + oth.lmax), res.rmax = Max(oth.rmax, oth.sum + rmax);
    res.lmin = Min(lmin, sum + oth.lmin), res.rmin = Min(oth.rmin, oth.sum + rmin);
    res.maxl1 = max({maxl1, -sum + oth.maxl1, oth.lmax + rmax * 2 - sum});
    res.maxl2 = max({oth.maxl2, oth.sum + maxl2, -rmin + oth.sum - 2 * oth.lmin});
    res.dat = max({dat, oth.dat, maxl2 + oth.lmax, -rmin + oth.maxl1});
    return res;
  }
};
Element L = Element{1, 1, 1, 0, 0, 1, 1, 1}, R = Element{1, 0, 0, -1, -1, -1, 1, 1,};

CF631E

假设现在交换了 $i, j$ 两个位置，记一个前缀和 $s_{i} = a [1 \dots i]$ ，操作后变化的代价是 $a_{i} (j - i) - (s_{j} - s_{i})$ ，拆一下变成 $(- a_{i} i + s_{i}) + a_{i} j - s_{j}$ ，可以直接李超线段树做了。

CF932F

写个式子先，定义 $d p_{u}$ 表示从 $u$ 跳出去的最小代价，那么有

\begin{matrix} (13) & \begin{array}{r} d p_{u} = d p_{v} + a_{u} \times b_{v}, (v \in subtree (u)) \end{array} \end{matrix}

直接李超树合并即可。

CF1860E

难过，赛时写了好久都没有过。😔

其实思路很简单，把相邻两个字符拎出来映射一下，但是边数过多，可以达到 $n^{2}$ 级别，于是把边权扩倍，建虚点即可。
跑 0/1 最短路就行了。

CF1860F

好题，但是没啥人补。
观察一下式子的形式 $a x + b y$ ，给定了一堆 $(a_{i}, b_{i})$ ，现在要求满足要求的 $(x, y)$ ，可以放到平面上，把这些二元组看成向量。
于是相当于按 $(a_{i}, b_{i})$ 和 $(x, y)$ 的点乘结果排序，于是现在假想一个动态的过程，一个向量绕着原点转一圈，查看是否能满足条件。
于是对于两个点对 $(a_{1}, b_{1})$ 和 $(a_{2}, b_{2})$ ，我们只用关心在某个时刻，他们的顺序会交换，那么拎出来每个会产生交换的向量 $(x, y)$ ，数量级是 $n^{2}$ 的可以接受，将它们按极角排序，思考一下，可以想到向量 $(x, y)$ 每变动一下产生修改的区间是一个连续的段（按该向量上的模排序），检验的方法很典，左右括号赋值，检验是否有前缀值小于 $0$ 即可。
于是此时直接将修改过的点拎出来，重新排序，然后塞回去即可，动态维护前缀值，只要小于 $0$ 的前缀个数为 $0$ 即可。
官方题解的代码非常优美，可以反复读一下。

int n; read(n);

vector<Bracket> p(n << 1);
for (int i = 0; i < (n << 1); i++) {
  read(p[i].a, p[i].b); char c; cin >> c;
  if (c == '(') p[i].c = +1;
  else p[i].c = -1;
}

map<Point, vector<int>> opt;
for (int i = 0; i < (n << 1); i++) {
  for (int j = 0; j < (n << 1); j++) {
    int x = p[i].b - p[j].b;
    int y = p[j].a - p[i].a;
    if (x <= 0 || y <= 0) continue;
    opt[{ x, y }].push_back(i), opt[{ x, y }].push_back(j);
  }
}
opt[{ 1, INF }];

vector<int> ind(n << 1), reind(n << 1);
iota(all(ind), 0);

sort(all(ind), [&](int i, int j) {
  LL di = dot({ INF, 1 }, p[i]);
  LL dj = dot({ INF, 1 }, p[j]);
  if (di == dj) return p[i].c > p[j].c;
  else return di < dj;
});
for (int i = 0; i < (n << 1); i++) reind[ind[i]] = i;

int neg = 0, now = 0;
vector<int> bal(1, 0);

for (int i : ind) now += p[i].c, bal.push_back(now), neg += now < 0;

bool res = neg == 0;
vector<int> pre;
for (auto it : opt) {
  vector<int> tot = pre;
  for (int x : it.second) tot.push_back(x);
  sort(all(tot), [&](int x, int y) { return reind[x] < reind[y]; });
  tot.resize(unique(all(tot)) - tot.begin());
  for (int x : tot) neg -= bal[reind[x] + 1] < 0;
  vector<int> tmp = tot;
  sort(all(tmp), [&](int i, int j) {
    LL di = dot(it.first, p[i]);
    LL dj = dot(it.first, p[j]);
    if (di == dj) return p[i].c > p[j].c;
    else return di < dj;
  });
  vector<int> nind(tot.size());
  for (int i = 0; i < tot.size(); i++) nind[i] = reind[tmp[i]];
  for (int i = 0; i < tot.size(); i++) reind[tot[i]] = nind[i];
  for (int x : tot) bal[reind[x] + 1] = bal[reind[x]] + p[x].c, neg += bal[reind[x] + 1] < 0;
  if (neg == 0) { res = true; break; }
  pre = it.second;
}

if (res) printf("YES\n");
    else printf("NO\n");

CF1858E1

比较简单，赛时就过了，一个经典的套路，把操作序列建建成树，回退相当于往祖先跳，跳 $k$ 步，这里倍增处理即可，统计答案用莫队的套路。

CF1858E2

第一想法是在 E1 的基础上加一个主席树，但是空间爆炸了。
其实如果没有 E1，我估计就会做 E2 了。😭
官方题解给的是开 $1 e 6$ 个 set 的弱智做法，本质上等同于主席树，但是不知道为啥空间能过，时间复杂度是 $Θ (n \log n)$ 的。
看了 jiangly 的代码，是 $Θ (n)$ 的线性牛逼做法，思路其实也很简单。

考虑一个字符如何贡献，我们关心的是出现了多少字符，意思就是字符集的大小，具体出现了多少次并不重要，我只需要知道每种字符第一次出现的位置就行了，很显然，这道题的所有操作都是在尾部进行的。

统计答案可以前缀和，维护操作序列 $A$ ，保证 $A$ 的前 $l$ 位是数字序列 $a$ ，加数非常简单，在末尾添加，这里注意第 $l + 1$ 位可能之前就有值（回滚回来到 $l$ 的），做法是先删掉 $l + 1$ 的贡献，然后添加当前需要加入的贡献。注意将此次操作修改到的元素加入栈中，方便还原。

read(val);
a.push_back({ val, pos[val], b[n], pos[b[n]], s[n + 1] });
if (pos[b[n]] == n) c[pos[b[n]]] -= 1, pos[b[n]] = q, c[pos[b[n]]] += 1;
if (pos[val] > n) c[pos[val]] -= 1, pos[val] = n, c[pos[val]] += 1;
s[n + 1] = s[n] + c[n], b[n] = val, n += 1;

删除操作直接回退就好了，也要将修改的信息丢入栈中。
建立在删除和添加操作上的撤销操作其实很容易，类似于可撤销并查集，从堆顶取出修改的信息，倒着做一遍操作，直接还原即可。

if (opt == '+') {
  read(val);
  a.push_back({ val, pos[val], b[n], pos[b[n]], s[n + 1] });
  if (pos[b[n]] == n) c[pos[b[n]]] -= 1, pos[b[n]] = q, c[pos[b[n]]] += 1;
  if (pos[val] > n) c[pos[val]] -= 1, pos[val] = n, c[pos[val]] += 1;
  s[n + 1] = s[n] + c[n], b[n] = val, n += 1;
}
else if (opt == '-') read(val), n -= val, a.push_back({ -1, val });
else if (opt == '!') {
  auto [x, y, z, w, t] = a.back();
  a.pop_back();
  if (x == -1) {
    n += y;
  } else {
    n -= 1, b[n] = z, s[n + 1] = t;
    if (pos[x] != y) c[pos[x]] -= 1, pos[x] = y, c[pos[x]] += 1;
    if (pos[z] != w) c[pos[z]] -= 1, pos[z] = w, c[pos[z]] += 1;
  }
} else printf("%d\n", s[n]);

CF1859E

好麻烦的题，做的时候想太复杂了。
$d p_{i, j}$ 表示前 $i$ 位，已经有了总长度为 $j$ 的段的最大值。
暴力转移是 $d p_{i, j} = max {d p_{i - 1, j}, d p_{i - x, j - x} + w (i - x + 1, i)}$ ，其中 $w (l, r)$ 表示当 $l, r$ 划分成一段时的贡献。
考虑优化，注意观察如果 $d p_{i^{'}, j^{'}}$ 能够转移到 $d p_{i, j}$ 那就说明 $i^{'} - j^{'} = i - j$ ，于是把 $x = (i - j)$ 即是说差值相同的归为一类。拆拆绝对值就能转移了。

CF1859F

看了 jiangly 传在 b 站上的视频，他用了点分治？？
遂查看官方题解，然后觉得评分确实虚高了。

其中一条 Hint 给得比较直接，它让我想想最优的路径长啥样子（Can you think how would an optimal answer path look like?）。

首先观察到学习的次数一定小于 $\log V$ 次，具体问题是学多少次，在哪里学？学多少次的范围是可以枚举的，于是解决在哪里学即可。

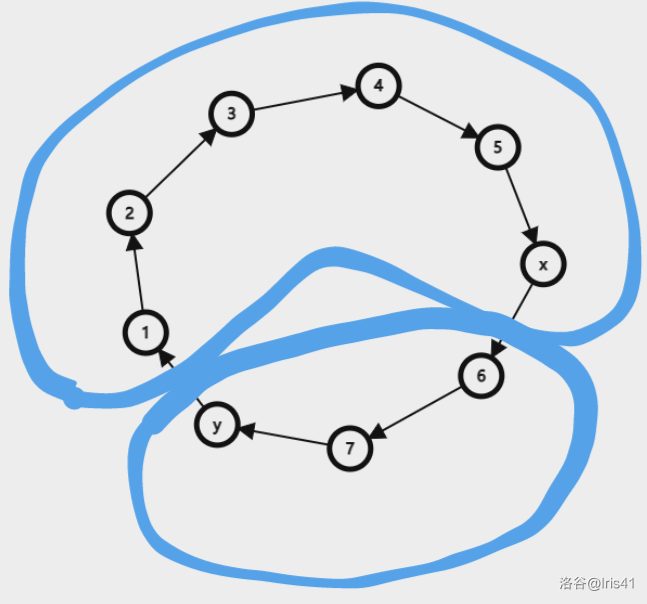
这下 Hint 就起作用了，如果在 $u, v$ 的路径间有学习点，一定会到最近的学习点学满枚举的次数，然后走剩下的路程，那如果没有学习点直接在路径上呢？
注意到题目允许多次走过某条路径，所以现在的路径看上去像是

会在路径上某个点离开向子树内走到一个学习点并返回，蓝色的路径是原长，红色的路径是在学习之后需要走的长度。

这就启发我们首先处理出来，每个从某个点出发学习 $k$ 次然后返回该点的最短路径，这一步多源最短路即可解决，记其为 $d_{k} (u)$ ，在学习了 $k$ 次的情况下，从根节点出发到当前点的距离 $d i s_{k} (u)$ 。

考察一条路径的组成，无非两种情况
在 $u \to l c a (u, v)$ 上找一个点 $p o s$ 出发去学习 $k$ 次然后返回路径经过 $l c a (u, v)$ 走到 $v$ 。
写出式子 $(d i s_{0} (u) - d i s_{0} (p o s)) + d_{k} (p o s) + d i s_{k} (p o s) + d i s_{k} (v)$ 。
而第二种情况反过来就变成第一种同样处理。

CF1856E2

😓，bitset 优化背包，但是我真的不会写，希望我多看看这份代码。

Accepted

CF1849F

讨论区有好多神仙做法%%%
但是还是选择看完了官方题解，因为里面有很多经典技巧（classical techniques）。

首先建出来这张完全图，对于 $i, j$ 以 $a_{i} \oplus a_{j}$ 的代价连边，划分集合就相当于对每一个点黑白染色，连接了相同颜色节点的边将会按连接的点的颜色计入代价计算之中。考虑当前二分了一个答案 $x$ ，那么对于所有边的权值小于 $x$ 的边，他们一定连接了不同颜色的点，于是判定二分图即可，然而不是很好加速这个进程。从贪心的角度去想，按边权从小往大加入，判断当前是否还是二分图即可，问题在于此时有
$n^{2}$ 条边，但是事实上，很多边是没有必要的，没有必要的含义是在加入这条边之后并不会影响整张图的状态（形态是否还是二分图或是否影响点的染色）。如果加入一条边连接了两个在同一连通块里面的点，出现下面这两种情况

这两个点颜色相同，这张图不再是二分图。
否则不会影响染色。

于是我们不会心一条连接在同一个连通块里面的边，每次都加入最小的连接不同连通块的边，或是说当前边打破了二分图的状态，停止操作。
这个过程很类似于 Kruskal，于是直接上异或最小生成树，在这个基础上染色就行了。

CF1864H

这是官方题解翻译，因为我也不会这道题，所以先翻译一遍。 /kk

首先有一个基础的 $Θ (n)$ 的 dp 解法。
在开始之前，令 $k = \frac{1}{2}$ ，因为在后续会有一个形如 $f (x) = a k^{b x}$ 的几何级数会被频繁使用到，并将它记为 ${a, b}$ 。

令 $f (x)$ 为表示从 $x$ 开始移动到大于等于 $n$ 的期望步数，显然，方程如下

\begin{matrix} (14) & \begin{array}{r} f (x) = {\begin{cases} 0 & n ⩽ x \\ k (f (x + 1) + f (2 x)) + 1 & x < n \end{cases} \end{array} \end{matrix}

很容易可以看出来，区间 $[n, 2 n]$ 中所有的 $f (x)$ 都是 $0$ 。

如果对于一个区间 $[2 l, 2 r]$ ，它已经可以被一些 ${a, b}$ 的和表示出来，那么它可以被在 $[l, r]$ 区间中更少的一些 ${a, b}$ 所表示。

首先，这里有 $f (r) = k f (r + 1) + k f (2 r) + 1$ 。所以 $r - 1$ 可以被表示为 $f (r - 1) = k^{2} f (r + 1) + k f (2 r - 2) + k^{2} f (2 r) + k + 1$ 。

类似地，可以得到

\begin{matrix} (15) & \begin{array}{r} f (r - x) = k^{x + 1} f (r + 1) + \sum_{i = 0}^{x} k^{i + 1} f (2 r - 2 x + 2 i) + \sum_{i = 0}^{x} k^{i} \end{array} \end{matrix}

换元一下，有

\begin{matrix} (16) & \begin{array}{r} f (x) = k^{r - x + 1} f (r + 1) + \sum_{i = 0}^{r - x} k^{i + 1} f (2 x + 2 i) + \sum_{i = 0}^{r - x} k^{i} \end{array} \end{matrix}

因为对于表示出 $f (r + 1)$ 的 ${a, b}$ 已经完全知道，所以可以很快计算出 $f (r)$ ，于是 $f (x)$ 的第一项可以被写出来。

\begin{matrix} (17) & \begin{array}{r} k^{r - x + 1} f (r + 1) = k^{r + 1} f (r + 1) \cdot k^{- x} = {k^{r + 1} f (r + 1), - 1} \end{array} \end{matrix}

然后对于 $f (x)$ 的最后一项 $\sum_{i = 0}^{r - x} k^{i}$ 是一个平凡的几何级数，所以运用开始定义的 ${a, b}$ 可以写成 ${2, 0} + {- k^{r}, - 1}$ 。

对于第二项 $\sum_{i = 0}^{r - x} k^{i + 1} f (2 x + 2 i)$ ，我们已经假设 $f (2 x + 2 i)$ 为 $\sum {a, b}$ ，所以把它拆开成如下的形式：

\begin{matrix} (18) & \begin{array}{r} \begin{aligned} \sum_{i = 0}^{r - x} k^{i + 1} f (2 x + 2 i) & = \sum_{i = 0}^{r - x} k^{i + 1} \sum_{f} {a, b} \\ = \sum_{i = 0}^{r - x} k^{i + 1} \sum_{f} a k^{b (2 x + 2 i)} \\ = \sum_{f} \sum_{i = 0}^{r - x} k^{i + 1} a k^{b (2 x + 2 i)} \\ = \sum_{f} \sum_{i = 0}^{r - x} a k^{2 b x + 1} \cdot k^{i + 2 b i} \\ = \sum_{f} a k^{2 b x + 1} \sum_{i = 0}^{r - x} (k^{2 b + 1})^{i} \\ = \sum_{f} a k^{2 b x + 1} \cdot \frac{k^{(2 b + 1) (r - x + 1)} - 1}{k^{2 b + 1} - 1} \\ = \sum_{f} \frac{a k^{(2 b + 1) (n + 1) + 1}}{k^{2 b + 1} - 1} \cdot k^{- x} + \frac{- a k}{k^{2 b + 1} - 1} \cdot k^{2 b x} \\ = \sum_{f} {\frac{a k^{(2 b + 1) (n + 1) + 1}}{k^{2 b + 1} - 1}, - 1} + {\frac{- a k}{k^{2 b + 1} - 1}, 2 b} \end{aligned} \end{array} \end{matrix}

有一个显然的结合律， ${a, b} + {c, b} = {a + c, b}$ ，它的几何级数和递归次数成线性关系。

对于 $x \in [n, 2 n], f (x) = 0$ ，可以被表示成 $f (x) = {0, 0}$ ，然后可以递归至能够生成 ${1, 1}$ ，得到答案。

复杂度取决于实现方法，为 $Θ (T \log^{3} n)$ 或者 $Θ (T \log^{2} n)$ 。

CF1868C

观察到 $m \leq 1 e 5$ ，所以考虑枚举每种 $s_{i, j}$ 。有最大值在其中，充斥比较好做，于是定义 $d p_{i}$ 表示对于每条路径，路径上的点的最大值小于 $i$ 的方案数量。
考虑子树如何拼答案，拆成左子树、右子树和根即可，这样满二叉树可以提前处理出来。

CF1863F

两个性质：

$x \otimes y = 0 \Rightarrow y = 0$
$x \otimes y < x \Rightarrow {highbit}_{y} (x) = 1$

考虑能被保留的区间之间的互相转移， $[l, k]$ 这个区间能从 $[l, r]$ 转移过来当且仅当 ${highbit}_{\otimes_{i = l}^{r} a_{i}} (\otimes_{i = l}^{k} a_{i}) = 1$ 。
可以 $Θ (1)$ 转移。

CF1863G

比较有意思。首先把 $i \to a_{i}$ 的边建出来，把交换操作放到基环树上面去。
形象一点理解，相当于把 $i$ 接在 $a_{a_{i}}$ 上面，同时 $a_{i}$ 变成自环，并且 $a_{i}$ 在后续无法继续操作，于是对树的形态计数。先不考虑环，那么方案数为 $\prod_{i \notin c} (in (i) + 1)$ ，至于环上的点，需要去重，方案数为 $\prod_{i \in c} in (i) + 1 - \sum_{i \in c} (in (i) + 1)$ 。

CF1864E

首先考虑有两个数 $a, b$ ，什么时候能猜出大小关系。

当 $a < b$ ，并且 ${bit}_{a} (i) = 0$ ，步数为 $i + 1 - (i & 1)$ 。
当 $a = b$ ，那么必须把 $a ∣ b$ 的位数都猜一边。
当 $a > b$ ，并且 ${bit}_{b} (i) = 0$ ，步数为 $i + (i & 1)$ 。

于是往 Trie 上塞即可。

CF1864G

非常神奇的题。
记操作了某一行后数字能回到正确的列上的行和操作了某一列后数字能回到正确的列上的行和列是可操作的。
如果当前同时存在可操作的行和列那么一定无解，因为这个时候会有一个格子会被操作两次以上。
结论是记录当前可操作的行、列，只要此时只存在一种，那么直接操作完需要操作的行、列即可。

CF1817C

一开始居然把题看错了，脑子有点晕。😵

现在把题搞清楚了，我来试试

\begin{matrix} (19) & \begin{aligned} \sum_{i = 0}^{d} b_{i} x^{i} & = \sum_{i = 0}^{d} a_{i} (x + s)^{i} \\ \sum_{i = 0}^{d} b_{i} x^{i} & = \sum_{i = 0}^{d} \sum_{j = 0}^{i} a_{j} (\binom{i}{j}) x^{j} s^{i - j} \\ \sum_{i = 0}^{d} b_{i} x^{i} & = \sum_{i = 0}^{d} x^{i} \sum_{j = i}^{d} (\binom{j}{i}) a_{j} s^{j - i} \\ \sum_{i = 0}^{d} b_{i} & = \sum_{i = 0}^{d} \sum_{j = i}^{d} (\binom{j}{i}) a_{j} s^{j - i} \\ ⟹ b_{i} & = \sum_{j = i}^{d} (\binom{i}{j}) a_{j} s^{j - i} \end{aligned} \end{matrix}

6，推不动了。其实直接代值进去即可。
令 $i = d - 1$

\begin{matrix} (20) & \begin{array}{r} b_{d - 1} = d \cdot a_{d} + a_{d - 1} \end{array} \end{matrix}

然后可以递推了。😂

CF512D

注意到这个操作有点类似于拓扑排序，唯一的不同是该操作在点的度为 $1$ 的时候就可以删去。
并且对于每个 $k$ 都要进行计数，那么考虑能否以上一层的答案来转移当前层。

观察样例发现有 $0$ 的出现，因为某些点根本删不掉，首先处理出来这些点，具体地，拓扑排序一次找出环上的点，然后把每个环看作一个已经连好的连通块。

因为 $n$ 比较小，可以想一些状态限制较多的做法，继续之前的想法，观察这张图，发现该图由很多颗树构成，每一颗树的答案是孤立的，如果树连在了环上，可以直接断掉，变成有根树，这样并不影响答案。于是先考虑一棵树计数。

如果是有根树，那么直接做一遍即可，如果是无根树，需要以每个点为根做一次，这样一种方案会被算 $s i z - k$ 次，树上转移方程是平凡的

\begin{matrix} (21) & \begin{array}{r} d p_{u, k} = \sum_{j = 0}^{k} d p_{u, j} \cdot d p_{v, k - j} \cdot (\binom{k}{j}) \end{array} \end{matrix}

然而我写了很久，果然我写有细节的代码能力欠缺。好吧，这个确实写起来有点恶心，我写了 3.4k 😭。

CF516E

首先判无解，只有当两个序列长度一样并且不是每个位置上都有 $1$ 就无解。

感觉很抽象，完全没有思路，留个坑，明天来填。

CF526G

首先一个很明显的观察是，选择的路径一定是从一个叶子到另一个叶子，显然，其中一定包含了直径。

注意到强制包含 $x$ 这个奇妙的限制。

CF573E

从一个 naive 的想法开始入手，定义 $d p_{i, j}$ 表示前 $i$ 个数选择了 $j$ 个数能取到的最大值，那么转移方程为

\begin{matrix} (22) & \begin{array}{r} d p_{i, j} = max {d p_{i - 1, j}, d p_{i - 1, j - 1} + j \times a_{i}} \end{array} \end{matrix}

直接转移是 $Θ (n^{2})$ 的，观察这个式子有何性质？

固定下 $i$ ，把转移式子里面的两个转移式写成函数的形式记为 $f_{i} (j) = d p_{i - 1, j}$ ， $h_{i} (j) = d p_{i - 1, j - 1} + j \times a_{i}$ 。这两个函数有交，考虑去二分这个交点然后更新答案。

于是得到现在的做法为维护一个序列 $r e s_{i}$ ，初始没有数，每次二分找到两个函数的交点，记作 $k$ ，在后面添加一个等于 $r e s_{k}$ 的元素，并把对 $r e s_{k}$ 以后的数加上一个等差数列。写平衡树上二分的话，复杂度是 $Θ (n \log n)$ ，一个比较优秀的写法是维护差分数组。确实非常好写。

CF576D

题面看起来很经典，从限制入手，如何转化至少走过 $d_{i}$ 条边？可以直接按照 $d$ 排序，维护转移的邻接矩阵和当前能够到达的位置，那么 $d_{i}$ 和 $d_{i + 1}$ 之间的转移直接做快速幂即可，注意到只关心可达性，于是可以用 bitset 优化矩乘。

CF1697E

怎么思维又开始僵了啊。
首先对于每个 $i$ 处理出来 ${s_{i}}$ 表示该集合里面的点 $j$ 满足 $d i s (i, j) = {min}_{k = 1, k \neq i}^{n} {d i s (i, k)}$ ，这样的话，在条件二的限制之下一定有：如果 $i$ 的颜色不是唯一的，那么 $i$ 就应该和 $j$ 同色，于是这时从 $i$ 向 $s_{i}$ 里面的所有点连边，拿到一张有向图。
对于每一个 $s t$ 作为起点，开始遍历，那么能遍历到的点都应该和 $s t$ 染上同样的颜色，如果染色集合里面存在了某对点 $(j, k)$ ，之间没有连边，就称这个 $s t$ 是孤立的，此时 $s t$ 必须单独一种颜色，否则称遍历到集合为合法集合。
于是对于一个合法集合，就有两种染色方式，一种是染上 $s i z$ 种，另一种是全部染上 $1$ 种，对于一个不合法的集合，就只能全部拆开，于是这是个背包。
然后组合数学算一下即可。

CF1681E

只能说有点疲倦了。
这个就是 ddp 的板题，写代码就当是提一下神。

CF1633E

怎么今天状态也很糟糕啊。熬夜太影响第二天了，况且半夜也调不出来代码，不知道我昨晚在想啥。/fn
这个一眼看上去就是 slope trick，注意到 $m \leq 300$ ，这也太送了吧。很明显，在 Kruskal 的过程中影响边的选择的是边权的相对大小，于是直接处理出来某两条边在哪个时刻会交换大小。这样会有 $m^{2}$ 个时间点，然后比较牛逼的是直接处理每个时间点的答案，这样是 $Θ (m^{3} \log m)$ ，总之可以过就是了。

从这道题开始，每道题会计写代码用时。

CF1661E

怎么感觉像是 ddp，不知道存不存在线性做法，但是 ddp 解决一切。

我秒了。

CF1398F

首先对一个固定的 $x$ 是非常好求答案的，直接贪心填即可。具体而言，从 $p o s = 1$ 开始，如果能填 $x$ 个同样的就填，否则 $p o s$ 跳到下一个不同的位置继续这个步骤。
思考对于 $x = [1 \dots n]$ 如何加速这个过程。
不怎么优秀的地方在于花了大量时间去寻找下一个能连续填 $x$ 个相同元素的位置。于是去预处理 $d_{i}$ 表示从 $i$ 开始不同时存在 0/1 的最长长度，那么答案的形式长成 $p o s_{1}, p o s_{2}, p o s_{3}, \dots, p o s_{k}$ ，其中 $\forall i \in [1, k], d_{p o s_{i}} \geq x, p o s_{i} - p o s_{i - 1} \geq x$ 。于是线段树二分即可，似乎常数有点大了，但是这确实是 $Θ (n \log n)$ 的。

CF1389G

感觉好困难的题，咋下手啊，这每一步都很有逻辑，只能说被教育了。
先把问题简单化，把边双缩掉，因为边双内的所有点一定可以通过定向互相到达，这样不会有代价产生，所以这个问题放到了树上。
考察关键点这个限制怎么去掉，注意到关键点的含义，它们是需要作为起点的，首先强制定一个关键点为根，然后对于一个内部没有关键点的子树，可以从最近的关键点一直定向过来，所以这些点和关键点的行为平行，可以直接缩在一起，于是现在树的形态就变成了只有叶子节点上有关键点，更确切的说，所以叶子节点都是关键点。
下一步是考察饱和点如何确定，在上述条件下，饱和点一定形成一个树上的连通块，且连通块内的边都是双向边，连通块外的边都定向为指向这个连通块的有向边。
然后这个可以换根 dp 了。

CF1380F

很简单啊，为啥调了这么久呢。
考虑再没有修改的情况下，直接 dp 即可，定义 $d p_{i}$ 表示以 $i$ 结尾时整个字符串分开的方案数。于是有

\begin{matrix} (23) & \begin{array}{r} d p_{i} = (a_{i} + 1) \cdot d p_{i - 1} + [a_{i - 1} = 1] (9 - a_{i}) \cdot d p_{i - 2} \end{array} \end{matrix}

于是这个转移只和前两项以及当前的 $a_{i}$ 有关，可以轻松用 ddp 维护，线段树上矩乘很套路。

CF1373F

应该好好反省了，我是做过 JOI 2022 蚂蚁与方糖那道题的，这道没弄出来确实是弱智。
首先拆环成链，这一步不多说，然后考虑霍尔定理推论，想着去枚举城市集合，其实不用，直接等价为每个连续区间里面的城市均能被满足，即是

\begin{matrix} (24) & \begin{array}{r} \forall [l, r], \sum_{i = l}^{r} a_{i} \leq \sum_{i = l - 1}^{r} b_{i} \end{array} \end{matrix}

这个直接前后缀极值维护一下就行了。

CF1366F

这题挺好的，首先观察答案路径长啥样，抛开走的次数有限制这个条件，考虑可以无限走，那么最优策略就是从 $1$ 开始，经过一些边，来到某条边 $x$ ，然后之后就一直在 $x$ 这条边上左右横跳。

注意到 $n, m \leq 2000$ ，记 $d p_{i, p o s}$ 表示走了 $i$ 条边走到了 $p o s$ 时的最大距离，这样是可以 $Θ (n m)$ 去求的，具体而言，重复 $i$ 轮，每次枚举走的边 $j$ 即可求得。

下面解决当步数大于 $n$ 时的情况，很明显，我们可以通过 $n$ 步到达这个图上的每一条边，这样就可以开始反复横跳，这个形式很简单，是一次函数，具体而言，假设我们花了 $s$ 轮，走到了第 $i$ 条边，之后开始反复横跳，那么对于远处的一个步数 $t$ ，走过的路径长度为 $d p_{s, i} + (t - s) w_{i}$ ，为了使形式更容易被处理，写成 $(d p_{s, i} - s \cdot w_{i}) + t \cdot w_{i}$ ，很明显，对于每一条边 $i$ ， $d p_{s, i} - s \cdot w_{i}$ 最大时最优，那么对于 $i$ 记截距 $b_{i}$ 为 ${max}_{s = 1}^{n - 1} d p_{s, i} - s \cdot w_{i}$ ，在 $t (t \geq n)$ 时的贡献为 $f_{i} (t) = b_{i} + t \cdot w_{i}$ ，似乎需要上凸包去求。

其实到上面就可以做了，但是用凸包麻烦了，更容易的做法是直接对于每个一次函数求出它的控制区间，这里控制区间定义为 $r g_{i} = [l, r], \forall t \in r g_{i}, f_{i} (t) > f_{j} (t)$ 。具体实现时直接枚举其他的所有一次函数，找出交点把控制区间夹逼出来。过程需要二分，于是总的时间复杂度为 $Θ (n^{2} \log V)$ 。

题目比较简单，过程十分精妙。

CF1366G

除了数据范围很糟糕以外，这题思路挺好。
首先有一个很显然的状态 $d p_{i, j}$ 表示用 $s_{i}$ 匹配到了 $t_{j}$ 需要的最小步数，于是有

\begin{matrix} (25) & \begin{array}{r} d p_{i, j} = min {\begin{cases} d p_{i - 1, j} + 1 \\ d p_{i - 1, j - 1}, s_{i} = t_{j} \\ d p_{i, j - 1}, s_{i} = . \\ d p_{l s t_{i}, j} \end{cases} \end{array} \end{matrix}

其中 $l s t_{i}$ 表示从 $l s t_{i}$ 开始只用执行 $s$ 可以一直清空到 $i$ 的最近的位置。
注意到这题不要去考虑删除 $[l, r]$ 这个区间需要的代价，因为这样去做一定会带 $\log$ ，而上面做法已经把所有情况包含进去了，正确性来自于 $l s t$ 是最近的一个满足要求的位置。

总之要学会使用原子状态去拼整个问题状态。

CF1312G

大概是全网唯一解。
这个转移的式子非常明显，记 $d p_{i}$ 表示走到字典树上 $i$ 节点需要的最小步数，于是

\begin{matrix} (26) & \begin{array}{r} d p_{i} = min {\begin{cases} d p_{f a_{i}} + 1 \\ d p_{a n c_{i}} + r k_{i} - r k_{a n c} \end{cases} \end{array} \end{matrix}

其中 $r k_{i}$ 表示遍历到 $i$ 时出现了多少个 $S$ 中的点。
这个可以直接上优先队列懒惰删除解决。复杂度 $Θ (n \log n)$ 实现难度和思维难度远低于其他所有解法。

GYM103202J

感觉很容易啊，考虑主席树合并，以每个权值为版本建立主席树，初始的时候 $r t_{0}$ 是满的，其他树是空的，区间内 $x$ 赋值成 $x + 1$ 就直接把版本 $x$ 的主席树合并到版本 $x + 1$ 的主席树上。
区间最值可以套个二分，所以合并时要注意保留 $x$ 版本里面的点不要删，总的复杂度 $Θ (m \log n \log V)$ 。

CF1359F

我需要反应更快一点，首先二分答案记为 $m i d$ ，然后对于一对车 $i, j$ 如果要在 $m i d$ 之内相撞，那么应当满足 $max {t_{i}, t_{j}} \leq m i d$ ，其中 $t_{i}, t_{j}$ 分别是 $i, j$ 到达这两条线交点的时间。
现在问题是如何更快地去 check，也就是说我需要很快地判断这 $n$ 条线段有没有交，发现似乎很麻烦。考虑去维护局面上当前存在的线段，先拆开，将一条线段分成两个端点，变成加入和删除两次操作，按纵坐标和斜率排序，每次在删除和加入时直接检查上下的线段是否与它有交即可。过程用 set 维护。

CF1354F

观察到 $n \leq 7.5 e 1$ 似乎很有搞头，从最后的局面入手，一定是会剩下 $k$ 张牌，记为 ${S}$ ，至少会有 $\sum_{i \in S} a_{i}$ 那么其他的牌如何造成额外的 $b_{i}$ 贡献呢？
然后我开始贪，想让 $b_{i}$ 造成尽量多的贡献，因为和牌数有关，并且需要时刻满足不多于 $k$ 张牌，所以 $b_{i}$ 前面的系数最多是 $k - 1$ ，这里就有个很抽象的东西，最后一张牌怎么弄，它肯定是最后被加进来然后不删掉，产生的贡献很特殊，所以先考虑把它 ban 掉，用 $n$ 的复杂度枚举解决，于是剩下 $n - 1$ 张牌，我要选 $k - 1$ 记为 ${S}$ ，造成贡献 $\sum_{i \in S} a_{i} + \sum_{i = 1}^{| S |} b_{i} \cdot i$ ，因为 $a_{i}$ 前面没有系数，所以把 $S$ 集合中的牌按 $b_{i}$ 从小到大往里面扔即可。然后再选出一个 ${T}$ （实际上不是选的而是固定的），里面的牌造成 $\sum_{i \in T} b_{i} \cdot (k - 1)$ 的贡献。
所以直接先按 $b$ 排序，定义 $d p_{i, j}$ 表示前面 $i$ 个数选出来了 $j$ 个在 ${S}$ 中，就可以直接做了，注意一开始要 ban 掉一个。

CF1354G

感觉很有意思，像是小学学的找次品问题。但是注意到装有礼物的盒子不保证重量相等。
先考虑一个步数很多的做法，首先随便分出来两个集合，然后现在的目标是先找出来任意一对石头，因为石头的大小是固定的，并且是最大的，应该可以比较好地去入手。然后发现 $k \leq \frac{n}{2}$ ，这意味着啥，这意味着我每次随机，都有至少 $\frac{1}{2}$ 的概率找出来是石头，每次更新最重的，如果跑 $k$ 次那么错误的概率就只有 $\frac{1}{2^{k}}$ 了，然后想啊想，我不会这个。
点开题解，第一篇就是马大师的，Orz。抱歉我完全没看懂。。。

正解很聪明了，每次都拿一个已知的全是石头的集合和另外一个大小一样的集合比较，如果不相等，则说明有礼物，我一开始想过，但是没想到可以倍增跳。
这样我最多跳 20 次就能找到第一个礼物，然后剩下的 30 次匀给找石头。

CF1334F

假设当前处理到了 $a_{i}$ ，并且 $a_{i}$ 这个数能和 $b_{j}$ 匹配，那么要让它匹配就得去枚举上一个和 $b_{j - 1}$ 匹配上的 $a_{k}$ 。代价是对于 $(k, i)$ 之间的数而言的。即是要删掉所有大于 $a_{k}$ 的数产生的贡献，然后对于小于等于 $a_{k}$ 的数，负的就直接加上。
假设这个贡献为 $w (k, i)$ ，于是式子就写成 $d p_{i} = min {d p_{k} + w (k, i)}$ 。
目标是解决算 $w (k, i)$ ，感觉形式不优美，需要二维数点，考虑再多去发现一些性质。

假设我从 $p o s$ 往后找（ $p o s$ 匹配 $b_{j - 1}$ ），找到 $x, y$ 都能匹配 $b_{j}$ ，钦定 $x < y$ ，寻找性质。~~我想放个图在这里但是我懒了 233。~~
首先， $y$ 后面的部分对于 $x, y$ 来说，都是一致的，贡献都是大于 $a_{x}$ 的数加上所有小于等于 $a_{x}$ 的负数。前面分成两个部分考虑，分别是 $[p o s + 1, x - 1], [x + 1, y - 1]$ 。
然后这里记两种区间贡献 $w_{1} (l, r, x) = \sum_{i = l}^{r} [a_{i} > a_{x}] p_{i}$ 和 $w_{2} (l, r, x) = \sum_{i = l}^{r} [a_{i} \leq a_{x} \land p_{i} < 0] p_{i}$ 则有

对于 $x$ ， $w_{1} (p o s + 1, x - 1, a_{p o s}) + w_{2} (p o s + 1, x - 1, a_{p o s}) + w_{1} (x + 1, y - 1, a_{x}) + w_{2} (x + 1, y - 1, a_{x})$ 。
对于 $y$ ， $w_{1} (p o s + 1, y - 1, a_{p o s}) + w_{2} (p o s + 1, y - 1, a_{p o s})$ 。

因为 $w$ 是具有可拆性质的，然后我拆。

对于 $y$ ， $w_{1} (p o s + 1, x - 1, a_{p o s}) + w_{1} (x, y - 1, a_{p o s}) + w_{2} (p o s + 1, x - 1, a_{p o s}) + w_{2} (x, y - 1, a_{p o s})$ 。

抵一下，剩下的

对于 $x$ ， $w_{1} (x + 1, y - 1, a_{x}) + w_{2} (x + 1, y - 1, a_{x})$
对于 $y$ ， $w_{1} (x, y - 1, a_{p o s}) + w_{2} (x, y - 1, a_{p o s})$

于是这就很舒服了啊，和 $p o s$ 位置没关系了，选择 $x$ 还是 $y$ 保留直接比即可。然后这是可以做到线性的。

CF1327F

注意 $k \leq 30$ ，看看能不能直接去枚举每一位，关键在于我要去刻画一段区间的与值恰好等于 $x$ 。
也就是说，对于 $x$ 所有为 $1$ 的位置上， $[l, r]$ 之间里面的所有数这些位置全为 $1$ ，而剩下的位置上不能全为 $1$ 。那么拆位做个前缀和，记 $p r e (k, i)$ 表示 $2^{k}$ 这一位上为 $1$ 到 $i$ 位置的前缀和。
然后来描述一个限制 $(l, r, x)$ ，应该为

\begin{matrix} (27) & {\begin{cases} p r e (k, r) - p r e (k, l - 1) = r - l + 1, & 2^{k} & x = 2^{k} \\ p r e (k, r) - p r e (k, l - 1) < r - l + 1, & 2^{k} & x \neq 2^{k} \end{cases} \end{matrix}

于是只要能算出每一位上合法序列的个数，那么乘起来就是答案。

然后我就开始乱想

现在的问题就是填 $0 / 1$ 序列，要求某些段全填或者某些段不能全填。首先把所有需要全部填 $1$ 的序列扣出来，这部分答案是固定的。只考虑剩下的不能全填的区间，因为有些位置被强制填了 $1$ ，所以不能去用区间长度刻画问题，要用还没有被填的位置个数刻画，为了简化问题，应该把完整包含其他区间的大区间去掉，这样问题是等价的。
首先对于每一个右端点，如果区间限制是 $0$ ，只需要考虑最近的左端点即可，否则是考虑最远的左端点，这样就保证了转移的确定性，

然后网上题解到这一步就结束了？？！！为啥我不会啊？

哈哈，被薄纱了，这个确实能做了。

定义 $d p_{i, j}$ 表示前面 $i$ 位最后一个 $0$ 放在 $j$ 上的方案数，动动脑子，把对于 $i$ 需要放 $0$ 的最后一个位置跑出来，于是得到了

\begin{matrix} (28) & {\begin{cases} d p_{i, j} = d p_{i - 1, j}, j \in [p o s_{i}, i) \\ d p_{i, j} = \sum_{j = p o s_{i - 1}}^{i - 1} d p_{i - 1, j} \end{cases} \end{matrix}

你发现这个可以双指针不用写 $\log$ 数据结构，复杂度就对了。

CF1891E

按相邻数的 gcd 分段，具体是，当 $a_{i}$ 和 $a_{i + 1}$ 的 gcd 不是 $1$ 的时候就新分一段，发现有 $1$ 的情况很麻烦，所以把 $1$ 也分开。
于是操作中间一个就修改了相邻的两个 gcd，贪心就好了。

CF1260F

搞我心态啊。做了整整一个上午。
考虑把颜色区间扔到数轴上然后扫描线，当前扫到的区间代表的点的集合就是一组合法的。
所以每次只需要考虑加入或者删除一个点答案的变化即可。

我直接开始了！考虑往一个集合大小为 $c n t$ 的点集里面加入点 $j$ ，并定义 $x_{i} = r_{i} - l_{i} + 1, p r o d = \prod x_{i}$ 。

\begin{matrix} (29) & \begin{aligned} \sum_{i = 1}^{c n t} \frac{p r o d \cdot x_{j}}{x_{i} \cdot x_{j}} (d e p_{i} + d e p_{j} - 2 d e p_{l c a (i, j)}) \\ = & (\sum_{i = 1}^{c n t} \frac{p r o d \cdot d e p_{i}}{x_{i}}) + (\sum_{i = 1}^{c n t} \frac{1}{x_{i}}) d e p_{j} - 2 \cdot (\sum_{i = 1}^{c n t} \frac{1}{x_{i}} d e p_{l c a (i, j)}) \end{aligned} \end{matrix}

然后后面那个是树剖经典题。代码抽象。放个链接。

CF1313D

被 Kidulthood 嘲讽了，嘤嘤嘤。
这个题就一句话，扫描线只状压维护最后 $8$ 个线段的交。

CF1379F2

第一步把每个 $2 \times 2$ 的小格子拼在一起我会，因为必须放 $n m$ 个，所以每个这样的小格子都要放一个。
然后下面的文字可以在所有题解里看到相同部分。
定义一个左上角不能填的四方格为 $L$ ，一个右下角不能填的四方格为 $R$ 。整个图不合法的条件是存在 $L$ 在 $R$ 的左上角。
这个东西用线段树维护每一行 $L$ 的最小纵坐标， $R$ 的最大横坐标。代码小清新。

CF1396C

首先明确，回退只会回退一层，然后状态是关键，需要去刻画的是当前层的 boss 还需不需要被打一下。
先找出所有打怪的策略

用 $a_{i} + 1$ 次 $r 1$ 先把小怪突突掉，然后打 boss 一次，遁入下一层
用 $1$ 次 $r 2$ 把所有怪打一下，这是小怪全 gg 了，boss 剩一滴血
用 $a_{i}$ 次 $r 1$ 把小怪突突掉，然后用一次 $r 3$ 狙死 boss

前两种会让 boss 留一滴血，这时需要再回来用一次 $r 1$ 。于是状态定义为 $d p_{i, 0 / 1}$ 表示对于第 $i$ 层扫了第一次后 boss 剩多少血。转移显然。